|
On a whole, free flight
fliers seem to have always been way ahead of the aerodynamic knowledge curve
than control line fliers and radio control fliers - especially when it comes to
competition. All modelers are concerned with the basics of stable flight by
building straight airframes with the proper center of gravity, but when you have
some real-time force being applied to correct for imperfect trim, twisted wings,
wind gusts, it is usually possible to obtain acceptable flights. The centrifugal
force of a control line plane flying in circles, constrained by the counter
poise (centripetal force) of the control lines, and the movable elevators allows
the pilot to keep the model on course. Radio control with at least elevator and
rudder and/or aileron can, with the input of a skilled pilot, compensate for a
host of aerodynamic perturbations that would otherwise upset the flight path.
Author Donald Foote in this "A Mechanical Brain for Catching Thermals" article
from the 1956 Annual edition of Air Trails magazine does a great job of
imparting knowledge on how to configure a free flight model to seek out and
exploit thermals. He explains the physics behind a swept wing's ability to
automatically turn toward rising air. That same mechanism would help R/C thermal
sailplanes. Take a look at the wing planforms on these
F3B competition jobs and see if
you notice what I do.
A Mechanical Brain for Catching Thermals
 By Donald K. Foote, Author of "Aerodynamics For Model Airplanes" and "Model Airplane
Engines" By Donald K. Foote, Author of "Aerodynamics For Model Airplanes" and "Model Airplane
Engines"
To expect a free flying model airplane to fly in extremely large circles until
it finds a thermal, then deliberately turn, fall right into the thermal and work
its way into the area of greatest thermal activity sounds like expecting a lot from
an airplane that has no pilot. But this is not only possible - a model can also
be made to turn away from a downdraft area and leave it far behind.
These seemingly impossible performances can be attained by using a swept-back
wing combined with a little adjustment trick. Once a modeler understands how sweep
back can be employed on a model airplane as a mechanical brain to cause the airplane
to seek out thermals and run away from downdrafts, he will realize that swept wings
are as important to models as they are to supersonic jet aircraft. Sound strange?
Keep reading.
A swept-back wing is one in which the mid-point of the chord at the tips is located
further back toward the tail of the airplane than it is at the center of the wing.
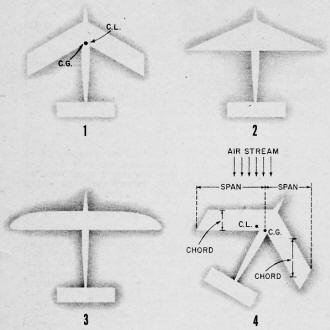
Figure 1 shows an airplane with a swept-back wing. In this illustration, the wing
has no taper and the wing tips are square in order to simplify and isolate the study
of sweep back. However, a wing with a straight trailing edge and a tapered leading
edge, as shown in Figure 2, also has the mid-point of its chord closer to the tail
of the ship at its tips than at its center and is, therefore, also a swept-back
wing. A modification of this in which the leading edge is tapered only at the tips
is shown in Figure 3, and is the design that I have found to work so exceptionally
well on models.
The wing shown in Figures 2 and 3 does not, of course, incorporate as much sweep-back
as a wing such as in Figure 1, but there is a practical limit to the amount to be
used, and the principles are just the same on all three designs.
A wing with sweep-back will stall at its tips sooner than it will at any point
closer to the fuselage. A tapered wing has this same characteristic and will also
stall at its tips sooner than a wing with no taper. This makes wings with sweep-back
and wings with tapered tips less desirable for full-scale lightplanes because the
ailerons become stalled out too soon and the result is loss of control.
However, it is this tip-stall characteristic of swept-back wings which makes
it possible to increase the soaring ability of models by causing them to turn into
a thermal and away from a downdraft. The wing tips of a model with a swept-back
wing in a normal glide are very close to the stalling point. By warping one half
of the wing so that its tip is flying at a slightly greater angle of attack than
the other, that wing tip will be on the very verge of a stall and if disturbed by
a thermal will stall out sooner than the other wing tip.
The greater drag on the wing tip with the larger angle of attack will make the
ship circle toward that tip in a normal glide. Therefore, this warp should be used
to adjust for a proper turn in the glide rather than using the dangerous adjustment
of turning the rudder. And, the airplane must be made to climb in the direction
of the wing tip with the greater angle of attack or a spiral dive might result during
the motor run at high speed.
When the airplane comes into the area of a thermal, the tip that is flying at
the greater angle of attack will stall out first. Lift will be destroyed on that
tip first, and the airplane will start a spin in that direction. Hence, it will
deliberately turn and fall off in the direction of the thermal. As soon as it regains
a little speed, it will stop its spin, but it will continue to circle tightly and
will tend to work toward the center of the thermal or the area of greatest thermal
activity.
Furthermore, when the airplane hits a downdraft the wing will suddenly be flying
at a lower angle of attack. Neither tip will be flying so critically close to the
stall. The difference in drag of the two will not be as great, but the difference
in lift of the two tips will become greater. The tip with the larger angle of attack
will now develop more lift than the other and the airplane will start to roll and
actually tend to turn in the direction opposite to its normal turn. Thus, it will
tend to turn and fly away from the area of the downdraft.
I cannot emphasize too strongly that this "mechanical brain for finding thermals"
really works like a charm. I have used it for more than a dozen years. But there
are two other characteristics of swept-back wings that should also be understood.
Lift, of course, is generated along the full span of the wing, from the fuselage
to the tip. But, just as the center of gravity can be considered as the point where
all weight is concentrated, so the center of lift can be considered as concentrated
at a point.
In Figure 1, suppose that the center of lift has been located as shown at the
point marked C.L. The center of gravity is also at this point. The center of gravity
would be behind the center of lift of the wing if a lifting tail were used because
the stabilizer would also contribute lift. In that set-up, to be in balance the
center of lift of the stabilizer added to the center of lift of the wing would make
the total center of lift of the airplane fall directly on the center of gravity.
But since we are not here considering the effect of lifting tails, we can assume
that the illustration is of an airplane with a non-lifting stabilizer. So, the center
of lift of the wing and the center of gravity of the airplane will lie at the same
point.
The airplane is also in balance laterally. That is, it is flying with the wings
level because both wings are producing the same amount of lift. Thus the center
of lift is at the midpoint between the two wing tips as shown.
In order to understand the effect that sweep back has on a model, it is necessary
to examine what happens in a slip. The slip is the fundamental maneuver of a model
airplane which is used to obtain its stability. When a model starts to turn in the
climb, it slips slightly towards the inside of the turn. Figure 4 shows an airplane
in a left turn. It is slipping toward the left causing the air stream to strike
it as shown. Actually, of course, the amount of slip is so small that it can hardly
be seen; in this illustration, however, exaggerations are made in order to show
the principles more clearly.
With the airstream hitting the left wing more directly perpendicular to the leading
edge than it does the right wing, the left wing will have an effectively higher
aspect ratio relative to the air stream. Thus, it will be more efficient and produce
more lift than will the right wing.
This will cause the left wing to rise and tend to roll the model to the right.
Or, in other words, to bring the model out of its left bank and prevent a spiral
dive. Another way of saying this would be to say that in a slip to the left the
center of lift is shifted to the left or lower wing causing it to rise. This is
illustrated in Figure 4.
It can also be seen in Figure 4 that the effective chord of the left wing is
shorter than the effective chord of the right wing. Yet, the thickness of the airfoil
is the same for both wings. Therefore, the constant of lift for the left wing is
greater than that for the right wing. This also causes a shifting of the center
of lift towards the left and tends to bring the model out of its banked attitude.
The sharper the turn in the climb, the more the airplane will slip and therefore
the stronger will become the force lending to bring the airplane out of its bank
and prevent a spiral dive.
Therefore, sweep-back does the same job that dihedral in the wing does, but without
the loss in wing efficiency that dihedral causes. For high speed, such as in the
climb, sweep-back is about 10% to 15% as effective as an equal angle of dihedral.
But, near the stall, it becomes about 30% or more as effective.
Just as the center of lift of a swept wing moves outward toward the tip of the
forward wing in a slip, so too does the center of drag. In Figure 4, it can be seen
that the left wing tip is further away from the center of gravity than the right
wing tip, giving it a favorable leverage and generating a greater moment of force
than the right wing tip.
The greater drag on the left wing will tend to swing the nose of the ship toward
the left. Sweep-back, therefore, has the same effect as vertical fin, or rudder,
area.
Sweep-back is, of course, nowhere near as powerful an influence for directional
stability as the rudder. Yet when considered as a factor to reduce the size of the
rudder, it becomes a very potent influence - especially on models, since it is important
to use a minimum of rudder area because the model must slip in order to gain lateral
stability.
One word of advice: Don't go to extremes. It doesn't take much sweep-back to
make your model act like it was controlled by a mechanical brain. Experiment a little
and you'll get soaring performance you never realized was possible from a pilotless
airplane.
Posted December 9, 2023
|



