|
By 1946, nobody had ever even
launched an unmanned rocket into outer space, much less a manned one. Nevertheless,
plenty of people were working toward it. With World War II having been over
for a year and much of the technology developed being applied toward future wars
and societal advancement, the dream of exploiting a presence in orbit around the
earth was hotly pursued. The world's superpowers were engaged in a race into space
both for prestige and military advantage. As is the case today, countries pretended
to get along well enough to cooperate on shared goals, but we all know behind the
scenes scheming was going on about how to apply lessons learned to the disadvantage
of "them" and to the benefit of "us." It is a survival of the fittest scenario.
Unfortunately, when you cannot trust "them" to not do the same to "us," offensive
and defensive plans are required - it has always been so and probably always will
be ...but, I digress. This article by Will Ley delves into some of the then-anticipated
issues that need to be dealt with in order to develop a presence in space - escape
velocity, weightlessness, life support systems, navigation, structural integrity,
propulsion systems, etc. Back in the day, there were still physicists that doubted
rocket engines could provide thrust in the vacuum of space (they must have skipped
class when Newton's third
law of motion was discussed). It is a very interesting read from beginning.
Outward Bound
 Article by Willy Ley Article by Willy Ley
Illustrations by Frank Tinsley
This control-room scene may be quite normal during flight outside the atmosphere.
The two-deck cabin is a pressurized cylinder with domed ends, similar to the forward
compartment of a B-29 set on end. The floor is a thick foam rubber mat upon which
crewmen lie prone during the initial acceleration. Spring loaded safety belts hold
them in position and two recessed panels carry the necessary controls. Near one
wall an airtight hatch leads to the airlock and outer door. Above it another hatch
gives access to the automatic instrument compartment. The ceiling is illuminated
by fluorescent tubes set in a cove above the instrument panel, and an air grill
in the center of the dome connects with the air conditioning system. The room is
walled with 24" panels, in which instrument groups alternate with stowage cabinets
and double paned ports. One port on either side is fitted with a retractable astro-dome
carrying a periscope which reflects a 360° view upon a series of recessed mirrors
which frame it. This. arrangement permits all around vision from any part of the
control room. When the ship has reached its final flight velocity gravitational
effects on the occupants disappear, and they float freely about the interior of
the cabin. A gentle push in any direction serves for movement, and rubber grab ropes
and foam rubber panel padding prevent injuries. In this scene, the astrogator is
braced upright, while the engineer changes a film magazine in a more convenient
upside-down orientation. The pilot, meantime, dozes comfortably in midair, exactly
like the relaxed citizen in present-day mattress ads.
 The picture on the cover is, of course,
a photograph of a captured German V-2 rocket rising from the White Sands proving
ground in New Mexico on a vertical 85-mile journey. If such a picture had appeared
twenty years ago, it would have been a still from Fritz Lang's "Girl in the Moon."
showing a spaceship on its journey to the moon. True enough, it was a movie spaceship,
a model only, but still one conceived by scientists. In another five years the cover
might well show a rocket taking off on a trajectory ending among the meteorite craters
on the moon, an unmanned rocket at first. But another ten or fifteen years after
that it will be a photograph of a real spaceship rising from some place dose to
the equator on its outward bound voyage. The picture on the cover is, of course,
a photograph of a captured German V-2 rocket rising from the White Sands proving
ground in New Mexico on a vertical 85-mile journey. If such a picture had appeared
twenty years ago, it would have been a still from Fritz Lang's "Girl in the Moon."
showing a spaceship on its journey to the moon. True enough, it was a movie spaceship,
a model only, but still one conceived by scientists. In another five years the cover
might well show a rocket taking off on a trajectory ending among the meteorite craters
on the moon, an unmanned rocket at first. But another ten or fifteen years after
that it will be a photograph of a real spaceship rising from some place dose to
the equator on its outward bound voyage.
The point I am trying to make is that the cover of today and the possible cover
of twenty years ago could be interchanged without too many people's noticing it.
And the probable covers of five and of twenty years hence will also look like the
one of today. The spaceship would be larger than the V-2 rocket, of course, but
size is indefinite when there is nothing but sky for a background.
Such predictions are easy to make these days. The idea of space travel is no
longer merely a subject of discussion among small and involuntarily exclusive groups.
It has even penetrated into official thought. During the first days of August, 1946,
a spokesman of the AAF told a conference of newspapermen in Washington that the
"AAF would place a guided missile on the moon." The statement that this would take
"about eighteen months" was either a mistake on the part of the spokesman, or a
bit of premature super-optimism, but it is nice to know that such thoughts exist
around the Pentagon. Just a few days before that announcement, Congress, while extending
to aircraft the law which makes mail coach and train robberies a federal offense,
saved itself future work by writing boldly "airplanes and rocket ships."
When hearing announcements of this kind those who failed to follow the admittedly
furious (and also largely secret) pace of rocket developments during the last few
years are apt to shake their heads and to ask how things could progress to such
an advanced point so suddenly.
The answer is, of course, that it was not suddenly, merely unnoticed. The contemporaries
of Columbus might also have felt that a great and important discovery had been made
"suddenly," since they did not know anything of the many years of planning and propagandizing,
of the incredible amount of discussions and disappointments, in short, of the decades
of work preceding the event which then became common knowledge.
Not quite three decades ago, in 1919, the now century-old Smithsonian Institute
published a thin book by Dr. Robert H. Goddard, a book in which it was stated that
it should be possible, under certain conditions, to send a rocket to the moon. A
few years later, a young student whose theoretical work was to lead to V-2 in the
years to come, published another thin book of some 80 pages. These 80 pages formed
an almost unbroken defensive position in the shape of a barbed wire entanglement
consisting of interlocking integral and square root signs, and from that fortified
position its author stated bluntly that not only the trip to the moon, but space
travel in general is possible. While the book was in print its author metamorphosed
from student into teacher and became known as Professor Hermann Oberth.
The book landed in the libraries (mostly unread) in the summer of 1923. Later
in the same year, on November 1st, Goddard coaxed the first liquid fuel rocket motor
of history into feeble and unreliable activity, obtaining a few pounds of thrust
for a few minutes. Twenty-one years (minus five weeks) after that date, during the
evening hours of September 8, 1944, the first operationally used V-2 crashed down
on Chiswick, London, from an altitude of 60 miles, its motor having delivered 27
tons of thrust for 71 seconds.
If two decades of work could trans form a small laboratory model of uncertain
value and performance into a 12-ton rocket with a 200-mile range, the moon does
not appear so distant any more. It appears hardly as distant as the shores of East
Asia were from European ports in 1450 - and though Columbus had long arguments about
the width of the ocean there is no argument about the gulf separating earth and
moon. Since the Army's radar experiment of a few months ago everybody even knows
the figure - 238,000 miles.
Even by terrestrial standards, it is not an impossibly long distance; just about
ten times around the equator. There must be thousands of locomotive engineers and
train personnel, captains and sailors, pilots and airline hostesses who have traveled
a greater distance than that. The difference, the awesome difference, is that even
Novaya Semlya to the North of Siberia, even Antarctica in the extreme South, are
still places on earth. The moon is not.
Let's Look at the Astronomical Situation
Its dominant characteristic is empty space. From far, far away come the white,
yellowish, bluish, and red lights of countless stars, other suns which are so far
away that no measuring system in daily use on earth, is even capable of expressing
their distances. The very nearest of them, our own sun, is 93 million miles away.
Around that sun our earth is moving, once in 365 1/4 days. The earth itself appears
as a compact ball, just below 8,000 miles in diameter. If you take those 8,000 miles
as a unit of measurement you still need thousands of such units to measure the distance
between the earth and its closest sister planets at the time of their closest approach.
But only 30 of these units away there is the moon, a much smaller globe, only 2,160
miles in diameter, fallowing the earth in the course around the sun. The two grip
each other with mutually interpenetrating gravitational fields.
Not counting occasional meteorites there is nothing solid between them. The earth's
atmosphere (the moon does not have one at all) does not count. It extends to just
about one. percent of the distance, being about 250 miles high. And only a few miles
at the bottom are useful for flying; Man is a deep-air animal and does not change
that status by climbing to 35 or 40,000 feet.
The airplane in which Man can climb to these "altitudes" (1/20th of one percent
of the earth's diameter) is also a "deep-air instrument." Its engines need the oxygen
of the air for combustion of the fuel; its wings need the flow characteristics of
dense air to lift its weight. The rocket is not in that class of vehicles depending
on the characteristics of a specific environment. Its motor does not need atmospheric
oxygen, because oxygen is carried along it) a special tank. The recoil or thrust
of the rocket's jet of fire is equally independent of its surroundings. In fact,
as external air pressure decreases, the thrust increases: the motor of V-2, capable
of delivering 60,000 pounds of thrust at sea level, produced 69,000 pounds at peak
altitude. Hence the complete and some what frightening emptiness of the space between
earth and moon is actually advantageous. One might say that a rocket, while independent
of its environment, does best in no environment at all, in interplanetary space.
Why Rockets Work in Space
 The perennial argument all rocketeers encounter
is, "How can a rocket work where there's no air or anything to push on?" Suppose
a standard welder's oxygen tank were somehow dropped in space, where there was no
air, and the valve opened. Inside the tank there is a pressure of 2,000 pounds per
square inch; outside, a perfect vacuum. Will the gas escape through the open valve?
Naturally. But - how can it? What does that gas push on to get moving outward, when
there's nothing to push on? But there is! It gets started outward by pushing on
the inner wall of the tank. Obviously, if the escaping gas pushes on the tank, and
the tank, being in airless space, has nothing to push on in turn, the tank simply
has to move. And if the gas doesn't push on the tank - how does it get started moving
out? The perennial argument all rocketeers encounter
is, "How can a rocket work where there's no air or anything to push on?" Suppose
a standard welder's oxygen tank were somehow dropped in space, where there was no
air, and the valve opened. Inside the tank there is a pressure of 2,000 pounds per
square inch; outside, a perfect vacuum. Will the gas escape through the open valve?
Naturally. But - how can it? What does that gas push on to get moving outward, when
there's nothing to push on? But there is! It gets started outward by pushing on
the inner wall of the tank. Obviously, if the escaping gas pushes on the tank, and
the tank, being in airless space, has nothing to push on in turn, the tank simply
has to move. And if the gas doesn't push on the tank - how does it get started moving
out?
Ideally, the rocket should, for maximum fuel economy, consume all its fuel almost
instantly. In this way, all the fuel energy would be used in accelerating the rocket
ship; no fuel-energy would be consumed in lifting tons of fuel to be used later.
The tin-can-and-firecracker system, in other words, is efficient, since the can,
but not the "fuel," is lifted. Machines can stand such an almost instantaneous start.
Human beings, however, can't take the tin-can take-off.
The human ideal, therefore, would be a rocket ship that took off slowly, with
a gentle acceleration like a freight elevator. Even modern high-speed elevators
are less comfortable than slower ones. But that brings up the fuel-energy problem.
A long-range plane uses two gallons of gas carrying the weight of the one gallon
that it must have at the end of its long flight; a slowly accelerating rocket ship
would have to use 10 tons of fuel lifting 1 ton for later use.
A compromise is necessary, and perfectly practicable. Men would like a 1-g take
off; the ideal rocket engine efficiency calls for a 1,000-g take-off. But men can
readily stand a 4-g start, and with that acceleration, the rocket ship is sufficiently
practical. The more energy-per-pound in the fuel, the slower the take-off of the
rocket ship may be. Atomic fuels will yield about 4,000,000 times the energy-per-pound
of gasoline-oxygen fuel, making elevator-slow takeoffs perfectly practicable. The
moon rocket ship is already possible.
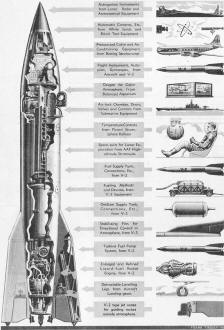
The artist shows here a hypothetical spaceship, based on the
V-2 design, and incorporating many fully tested devices and principles. The hull
is essentially a cylindrical, stressed skin structure, 80' long and 10' feet in
outside diameter. It is double walled, with very efficient insulation. The extreme
nose contains a series of glass fiber parachutes to be used for vertical stabilization
in atmospheric landings, with actual deceleration effected by the main jet. Below
the chute hold is space for recording cameras, cosmic ray detectors, and other instruments.
Beneath this is the upper deck of the pressurized control cabin. Next is a compartment
packed with mechanisms; autopilot, gyrostabilizer, air and temperature control plant,
radio and radar installations, etc. An airlock gives access to the outside through
a two-piece door, the lower port of which serves as a platform when open. Below
the crew space the fuel and oxidizer tanks occupy more than a third of the ship's
length, and beneath them is the rocket engine, with its pumps and plumbing. Worm
gear driven tubular legs in the fins permit leveling the ship on rough ground for
the return take-off.
If the emptiness of interplanetary space permits the rocket motor to work at
its best, it also does not impede the movement of the rocket itself. But before
interplanetary space is reached, the rocket has to traverse the atmosphere and it
is at this point that another inherent advantage of the rocket becomes obvious.
A rocket can acquire very high velocities, higher than the velocities of high-velocity
artillery projectiles. But unlike those projectiles, the rocket acquires its high
velocities gradually. It is easy to say that a projectile, fired vertically with
such and such a muzzle velocity, would reach interplanetary space and, if aimed
correctly, the moon. That is easy to say, but the facts of reality are that it wouldn't.
Any projectile moving with a velocity of several miles per second would encounter
such incredible air resistance that all its energy would be used up producing shock
waves.
A rocket accelerates gradually; to the great good fortune of rocket designers
it is slowest near sea level, where air density is highest. As the velocity of the
rocket increases, the air resistance decreases (assuming a vertical or near vertical
path); it might be possible to find an acceleration for the rocket where the two
factors, the increase of rocket velocity and the decrease of external air resistance,
balance each other at least approximately. Once the densest layers have been passed
the velocity could increase faster, the acceleration could go up.
Strangely enough, a rocket of sufficient size takes care of even that condition
automatically. If we say, for example, that a rocket weighs ten tons at take-off
and its motor produces a thrust of 20 tons it will rise with an acceleration of
1 gravity, or 1-g, for short. Its rise will be a reversed fall, its velocity upward
would increase in precisely the same measure as the velocity downward of a falling
stone would increase. It would increase in precisely the same measure, that is,
if the weight of the rocket remained unchanged. But, of course, the weight does
change, fuel is being used up steadily. After some time the rocket will weigh only
five tons, but the thrust of the motor will still be 20 tons (actually, because
of the effect mentioned earlier, it would he about 23 tons, but we'll ignore this),
hence its acceleration will then be 3-g. This increase in acceleration is literally
"just what we wanted," - we only have to watch out that it does not happen too early.
(Just for the sake of illustration it may be mentioned that the acceleration of
V-2 at take-off is slightly higher than 1-g, while the acceleration near the end
of the burning period is about 8-g.)
We can get a good idea about the altitude where the rocket might begin to be
really fast from an observation made over a decade ago. When the Stratosphere Balloon,
Explorer II, hovered at its peak altitude of 72,395 feet on November 11, 1935, the
men in the airtight spherical gondola had 24/25th of the total mass of the atmosphere
under their feet. Since the height of the atmosphere is customarily taken to be
about 250 miles, there were still about 1,200,000 feet of so-called air above the
balloon. But that million feet amounted to only 1/25th of the total mass.
Taking all the foregoing fads together we can safely conclude that the natural
performance of a rocket, functioning" as a plain rocket unhampered by wings, is
such that it may be expected to penetrate the atmosphere and to reach interplanetary
space. Provided, of course, that it is large enough.
There is just one point where we may wonder a little bit. Our conditions are
that the final velocity must be high, that the final acceleration should be high
(it should be high as far as the rocket itself is concerned, hut there is an obvious
limit to the acceleration if the rocket is a spaceship. i.e. if a man is to be carried),
but that the velocity must be fairly low at take-off and until the dense layers
of the atmosphere have been penetrated. The question is: Is there such an acceleration
which will combine these features?
That question can only be answered by calculations, by trying a few likely accelerations
and seeing how they work out. If we pick an effective acceleration of 3-g and, for
the sake of a quick first approximation, assume that the acceleration will not change
and that there is no air resistance, we find that the rocket, after twenty seconds
of burning, will be at an altitude of about 20,000 feet, moving at the, end of the
20th second with 1,900 feet per second. The latter is less than the velocity of
an artillery projectile - in short, the acceleration of 3-g effective just before
fills our needs.
Now we can look at the problem of the guided missile to the moon, as an introduction
to the problem of the spaceship to the moon. The essential difference between the
two is that the latter is manned, which imposes a limitation on acceleration. The
complicating point is that the spaceship is expected to come back, while the fate
of the missile is not so important.
The first question is not how big the missile would have to be, but how fast.
We can approach that question by looking at a well-known device, the anti-aircraft
gun.
Everybody knows by now that the altitude to which an anti-aircraft shell will
carry depends on the muzzle velocity of said anti-aircraft shell. The higher the
muzzle velocity, the higher the altitude reached. If air resistance did not confuse
the issue, a simple and clear relationship would be obvious: The muzzle velocity
required to fire a shell to an altitude of, say, five miles, is the same figure
as the impact velocity of a bomb dropped from an altitude of five miles. If somebody
could drop a bomb from the distance of the moon - which is large enough to be called
"infinity" for purposes of calculation - its impact velocity would be 11,200 meters
per second, which happens to be almost precisely 7 miles per second. Conversely,
to send a missile to that distance requires a velocity of 7 miles per second.
This is what the missile designer has to strive for; at least, it is the most
efficient way by far to make the missile attain that velocity as soon as possible
after the densest layers of the atmosphere have been traversed. Once that velocity
has been attained no further power application is required; the missile will go
on coasting with slowly diminishing velocity. We will look at that phenomenon more
closely a little later.
Naturally, nobody will try to sit down with a logarithm table (the slide rule
is not good enough for these calculations) ,and handbook and make plans for a moon
missile; neither "Mr. Wright nor Monsieur Bleriot sat down to design a B-29. There
will be many intermediate steps and a look at probable intermediate steps is interesting
because it will show what a little more velocity will do.
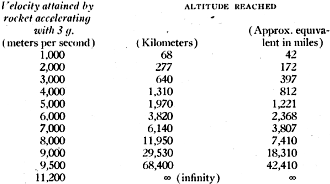 In the following table it is assumed that
a rocket which has an acceleration of 3-g is permitted to burn until it has reached
the velocity in the left hand column; the right hand columns then show to what altitude
it would coast before falling back. (Air resistance has been ignored.) In the following table it is assumed that
a rocket which has an acceleration of 3-g is permitted to burn until it has reached
the velocity in the left hand column; the right hand columns then show to what altitude
it would coast before falling back. (Air resistance has been ignored.)
To reach the velocity of 11,200 meter per second, or 7 miles per second, that
particular rocket would need a burning time of about 8 minutes, say 500 seconds
for the sake of getting a round figure.
What Then?
After having burned 500 seconds the rocket is far above what is euphemistically
called the fringes of the atmospheres. It is in empty space, traveling without power
now. Without any other power, that is, than its kinetic energy, the product of the
square of its enormous velocity and of half of its mass. There is no air resistance
anymore to slow it clown, but there still is the earth's gravity, trying to pull
it back.* It loses some 30 feet per second of velocity for every second that elapses.
It is no longer the full force of close to 32 feet per second per second which holds
true at sea level; it is already somewhat less. And it grows less and less as the
distance from the earth increases. In due course, the loss of velocity for every
second elapsed amounts to only 28, 27, 26, 25 feet per second, later to 16 15 14
13 feet per second, still later to only 6. 5. 4, feet per second. After 300,000
seconds have gone by, things approach a balance. The velocity losses are down to
fractions of an inch per second now, the velocity of the missile is down to a few
feet per second.
But by that time the point has been reached where the gravitational fields of
the earth and the moon, interpenetrating each other, as gravitational fields have
a habit of doing, are about equally powerful. Theoretically, there is a line where
they balance each other perfectly. Whether the ship crosses that line or not, it
will begin to fall after about 300,000 seconds after take-off. The only difference
is this: If the ship, or missile, still has enough velocity left to cross the line
of perfect balance, it will fall toward the moon.
If it fails to cross. the line, it will fall back to earth, entering the atmosphere
with 7 miles per second after about 300,000 seconds. But we'll assume that it did
cross the line and falls in the moons gravitational field. It will need 50,000 seconds
to get to the moon from the line of equal gravitational force and crash with an
impact velocity of 2,370 meters per second or 1.45 miles per second. From take-off
to crash there would be total time interval of 350,000 seconds, or about four days.
Looking at this performance, we now realize why it is more efficient to reach
the so-called "escape velocity" of 7 miles per second fast. There is always the
earth's gravity, trying to pull the missile back. If somebody decided that the-rocket-motor-is-after-all-very-powerful
and why-strain-the-ship-with-high-acceleration, consequently let's-take-it-easy-and-just-burn-a-little-more-fuel,
he would run no other risk than not getting anywhere. To begin with, the efficiency
of the rocket motor itself depends to a very great extent on the velocity of the
rocket. If the acceleration is kept low and the velocities stay low the efficiency
of the rocket motor stays low too. It means nothing more serious than higher fuel
consumption. More important even, the rocket would linger for a much longer time
in regions where a higher gravitational pull would cause much greater velocity losses.
The fundamental difficulty involved can be seen most easily by going to extremes.
Suppose the rocket pilot decides to maintain just a normal 1-g acceleration from
take-off. At the end of twenty minutes his fuel is exhausted - and the rocket will,
of course, be at an altitude of 0.00 miles, and the rocket's velocity will be 0.000
miles per sec. He has expended all his fuel in simply holding the rocket at a fixed
altitude against Earth's gravity.
Taking the other extreme, suppose the pilot of the rocket is a mechanism built
like the V-T fuse mechanism used in artillery shells, a device that can function
happily at 20,000-g accelerations. This mechanical pilot wouldn't mind burning all
the fuel almost instantaneously and executing a take-off at 20,000-g. When this
pilot's fuel is all gone, the rocket will still be only a short distance from the
ground - but it will be traveling at terrific speed. In this case, none of the energy
of the fuel will have been used in lifting part of the fuel; all of the fuel energy
will have been used in accelerating the rocket.
There is literally no upper limit to the fuel consumption which would be caused
by trying to keep the velocity low. The whole problem bears a strong resemblance
to the problem of carrying a leaking container of liquid to an upper floor in a
house. The slower it is done, the more of the liquid will leak away before it gets
to the point where it will do some good.
Fine, But What Is the Fuel Consumption?
There is no single answer to that question; there are a lot of them.
It depends on the fuel, or, more precisely, on the exhaust velocity of a fuel.
The solid powder bars used in bombardment rockets produce an exhaust velocity of
about 3,300 feet per second (1,000 meters per second), or a little better. The alcohol-water
mixture in V-2, burning with liquid oxygen, produces an exhaust velocity of close
to 7,000 feet per second (slightly above 2,000 meters per second). Hydrogen burning
with oxygen can be expected to produce about 4,000 meters per second. There exists
a substance known as "monatomic hydrogen," which is hydrogen where two atoms do
not form a molecule of hydrogen as usual, but where they are (very temporarily)
single atoms. Theoretically, that substance would produce an exhaust velocity of
20,000 meters per second; actually, one might expect about 10,000 meters per second.
But so far nobody has succeeded in producing monatomic hydrogen and keeping it in
that condition, and nobody knows how it could he stored if large amounts could be
produced.
It is obvious that a ton of fuel with a higher exhaust velocity will impart a
higher velocity to a rocket than a ton of fuel with a lower exhaust velocity; what
is needed at this point is a kind of permanent yardstick for purposes of comparison.
That yardstick is found in the ratio:
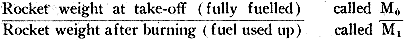
and the ratio M0/M1, is generally called "mass-ratio."
The yardstick is the exhaust velocity itself for a standard mass-ratio and the most
useful standard is, obviously, the mass-ratio where the rocket velocity becomes
the same as the exhaust velocity. The V-2 weighs about three times as much at take-off
than it does after all the fuel has been burned.
 By means of a mathematical formula * it
is possible to calculate the mass-ratio which is needed for attaining a desired
velocity, provided you know the exhaust velocity of the fuel. For the moon missile
we have a desired velocity of (in round figures) 12,000 meters per second. the 11,200
meters per second mentioned earlier plus some extra velocity for overcoming air
resistance. Assuming a set of exhaust velocities we can then write the following
table: By means of a mathematical formula * it
is possible to calculate the mass-ratio which is needed for attaining a desired
velocity, provided you know the exhaust velocity of the fuel. For the moon missile
we have a desired velocity of (in round figures) 12,000 meters per second. the 11,200
meters per second mentioned earlier plus some extra velocity for overcoming air
resistance. Assuming a set of exhaust velocities we can then write the following
table:
By sheer coincidence. the table contains a mass-ratio which IS that of V-2, the
figure 3.2. But the exhaust velocity belonging to that mass-ratio is 10,000 meters
per second, about 32,800 feet per second. If we had a fuel with such an exhaust
velocity a V-2 could reach the moon. With the actual exhaust velocity of V-2 it
is a sheer impossibility. There is no way of building a rocket that will weigh 402
times as much when fuelled as it weighs when empty. The 7.4 (to 1) mass-ratio which
belongs to the 6,000 meters per second exhaust velocity might still be built as
a single rocket and possibly, just possibly, even the 11-to-1 mass-ratio belonging
to the 5,000 meters per second exhaust velocity.
This would be most comforting if we could attain such an exhaust velocity by
the use of chemical fuels. But while we may hope for such fuels or hope for an application
of atomic energy, we have, as of August, 1946, to face the fact that 4,000 meters
per second is all we can expect to get, burning hydrogen with oxygen. The mass-ratio
belonging to that exhaust velocity is 20 to 1. It cannot be built as a single rocket,
but it can be built as a so-called step rocket, one rocket carrying another one,
only the second rocket, the "upper step" reaching the goal. (The Nazis planned the
"America Rocket" on that principle.)
In a step rocket the velocities attained by the single steps add up; it is the
same, in effect, as if the individual mass-ratios were multiplied. Hence (with a
little simplification) , if you have a lower step with an effective mass-ratio of
5 to 1 and an upper step with 4 to 1, the result, we'll call it "ideal mass-ratio,"
will be 20 to 1.
We can build such mass-ratios after some practice and experimentation. We can
also, again after some practice and experimentation, count on an exhaust velocity
of 4,000 meters per second.
Because of these two facts the guided missile to the moon is a distinct possibility.
* The formula reads: M0/M1
= ev/c
where v is the desired velocity, c the exhaust velocity (available or assumed)
and e the base of the so-called "natural logarithms." If v = c the ratio becomes
simply e = 2.71828; v = 2c the mass-ratio becomes e2 (7.4); if v = 3
c the mass-ratio becomes e3 = 20.0 etc. etc. The reader will have to
accept my assertion that this relationship actually holds true, proof is rather
difficult and space-consuming. As for the value of e, it is the result of a mathematical
series, but it can also be derived in a rather amusing elementary manner, by way
of "progressive percentages." If you take the figure 100 to begin with and add one
percent of it you get 101. Now you add another one percent, but not on the original
base 100 but on the new base 101. You get 102.01. Add one percent of 102.01 to that
and continue in the same manner until you have added one percent one hundred times
on that progressive base. The result of the addition will be 271.828 ...
* Contrary to an ingrained popular belief, the earth's gravitational field does
not stop at one point; it goes on and on into infinity. Of course, at a sufficiently
large distance it will get so weak that it can be ignored. If the case earth-moon
is under consideration, the earth's field "stops" when that of the moon becomes
more powerful.
Posted March 14, 2020
|