Airfoils and Alternatives - The "Skinny Lifters"
December 1974 American Aircraft Modeler

December 1974 American Aircraft Modeler Table of Contents These pages from vintage modeling magazines like Flying Aces, Air Trails, American Modeler, American Aircraft Modeler, Young Men, Flying Models, Model Airplane News, R/C Modeler, captured the era. All copyrights acknowledged.

Airfoils and Alternatives - The "Skinny Lifters"

This month's column was born on a beach. You're expecting maybe a few words on slope soaring? Sorry, the real origin of this month's effort is due to bikini watching. Plain and simple, the message this time is that the thickness of an airfoil is really like a bathing suit - both are used to cover the structure. And neither adds to the performance of the curved section.

To prove the point aerodynamically, we'll produce a new airfoil that could be used as a substitute for the NACA 6408 or 6409. It will have all the good lift characteristics of these sections, but much less drag. To prove the point anatomically, we'll have to wait until AAM comes up, with a centerfold (We're working on it. All interested females drop the Editor a line).

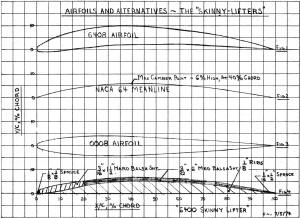
Click for 4x version of Skinny Lifters airfoil plots

Let's run through the NACA numbering system. All airfoils in the NACA four-digit series have, naturally, four digits as their title. The first number gives the amount of max camber in percent chord. The second gives the location of the max camber point in tenths of chord length. The last two digits give the max thickness in percent chord.

NACA 6408, for example, would have 6% max camber located at 40% of the chord from the leading edge, and would be 8% thick. Fig. 1 gives a sketch of the airfoil. Fig. 2 shows the mean line of this section. Remember that the meanline is the curved line that goes right through the middle of the airfoil. Note that, as advertised, the NACA 6408 meanline has a max height of 6% of chord length which is located at the 40% chord location.

So much for the four-digit numbering system. Now comes the meat. During the past few months, this column has been making new airfoils by modifying older proven ones. I've talked about splitting airfoils up into rneanlines with thickness distributions, altering the max camber and the max thickness, and adding them back together again to get the new sections.

The problem has been that this is about as clear as mud unless you've had some experience at it. Since the basic aim of AAM is to explain, not mystify, this month we'll take the space to layout how it is actually done. This will accomplish two things: first, you'll be able to make your own airfoils, and second, you'll get some understanding of why the "Skinny Lifters" ought to work out and how to make them.

Let's start with the NACA 6408. There are tables available in the four-digit series that give coordinates for the meanlines, depending upon where the max camber is located. In the master tables, all are given with a 6% camber. For modelers, the ones of interest are those ranging from 30% to 50% chord for the max camber location. This means the 63, 64, and 65 mean lines. The master tables, as I call them, are included in this article.

Here's where the flexibility comes in. Suppose that what you want is an airfoil with a 44 meanline instead of a 64. To get the 44 meanline all you do, if you don't mind the effort, is to take all the height coordinates of the 64 and multiply them by the ratio of the desired camber divided by six. For example, at the 20% chord location, the 64 mean line height is a 4.50%. Multiplying 4.50 by 4/6 gives 3.00 as the height of the 44 meanline at the 20% chord location. If you really want to get into the design of things, the design lift coefficient, moment coefficient, and design angle of attack (lowest drag) are also found by multiplying the 64 values by the same ratio of 4/6. If you wanted to make a 74 meanlined section, you'd multiply the 64 values by 7/6.

The point is that the meanlines of the NACA four-digit sections can be raised or lowered by simple multiplication. It takes effort and patience, but it's no big technical problem. Worth noting here is that once you know what your meanline is going to be or is, this is what describes the lift characteristics of the airfoil.

If you look at the meanline of the 6408 section in Fig. 2, it's simply a line. If you could build an airfoil of sheet metal and hold that shape, you could place it on any wing using an NACA 64 meanlined airfoil. You wouldn't have to change angle of attack, or anything. The airplane would just fly flatter in the glide, or faster if it were a powered ship. The catch in this, of course, is that you can't build a zero thickness airfoil (on out-door ships anyway). The bather usually needs a bathing suit, right?

Our aerodynamic bathing suit is the symmetrical airfoil. It's used to keep spanwise spars and struts covered, because they would really be drag makers in the open breeze. To avoid interfering with the airfoil lift characteristics, the way the symmetrical section is put on is to numerically add the upper half to the mean line, then subtract the lower half from the meanline. For lift purposes, you've done nothing to the airfoil. But, you have increased the drag, as compared to that curved sheet metal meanline that would do the same job.

To illustrate quickly how this is actually done, let's take the NACA 6408 at the 20% chord location again. The meanline height was 4.5%. F rom the tables in this article, the 0008 airfoil has a height of 3.83 or 8.33%. The 6408 lower surface becomes 4.50 minus 3.83 or .67%. (Author's note: For modeling - such as under one foot in chord length - this method of constructing an airfoil is accurate to within 1/32". For super accurate work, which is beyond most model building tolerances, the symmetrical section's coordinates should be laid off perpendicular to the meanline. At any rate, that's how I do it and most of my ships fly without any drastic alteration required for trim.

For what it's worth, one more point of NACA four-digit flexibility should be noted. The geometrics of symmetrical sections are all directly proportional to each other. By getting the coordinates on one, you can calculate exactly the coordinates for any other thickness. The height values of the 0006, for example, can be obtained simply by multiplying all the values from the 0008 by the ratio 6/8.

Now for the "Skinny Lifters" - or how to fly with hardly any bathing suit at all. A "Skinny Lifter" is simply a meanline made from sheet material in the middle with hard leading and trailing edges to avoid the rat-nibbled look. A section made this way is unlike a Jedelsky, in that the sheet is curved by tossing in ribs every three to four inches. The "6400 Skinny Lifter" shown in Fig. 4 is an attempt at an NACA 6400 airfoil. This section would be a good substitute for any 6409 airfoil. Its profile drag should be about 40% less than that of a 6409 and its installed performance might be good enough to give you a sailplane with 20% or so longer endurance.

If you wanted to try for a 6500 series section, for example, just use the 65 meanline shown in the chart. The important thing is to preserve the meanline shape by making the sheet of a thickness so that it just brackets the desired mean line.

Posted January 2, 2011